二叉堆是一组能够用堆有序的完全二叉树排序的元素,一般用数组来存储。
大顶堆, 每个结点的值都大于或等于其左右孩子结点的值,其顶部为最大值。
小顶堆,每个结点的值都小于或等于其左右孩子结点的值,其顶部为最小值。
二叉堆
性质
- 根节点在数组中的位置是 1
- 左边子节点 2i
- 右子节点 2i+1
- 父节点 i / 2
- 最后一个非叶子节点为 len / 2
- 根节点在数组中的位置是 0
- 左子节点 2i + 1
- 右边子节点 2i+ 2
- 父节点的下标是 (i − 1) / 2
- 最后一个非叶子节点为 len / 2 - 1
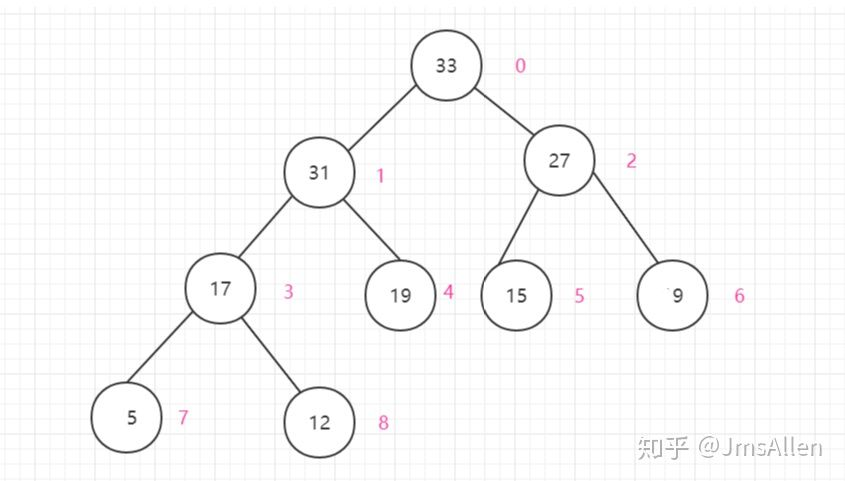
图片来自知乎
实现
构造二叉堆
- 找到最后一个非叶子节点 ( len / 2 或者 len / 2 - 1)
- 从最后一个非叶子节点下标索引开始递减,逐个下沉
插入节点
- 在数组的最末尾插入新节点
- 将最后一个节点上浮,时间复杂度为O(log n)
- 比较当前节点与父节点
- 不满足 堆性质* *则交换
删除根节点
删除根节点用于堆排序
对于最大堆,删除根节点就是删除最大值;
对于最小堆,是删除最小值。
- 交换根节点和最后一个节点
- 将此时的根节点下沉,时间复杂度为O(log n)
- 比较当前节点与子节点(左,右)
- 不满足 堆性质 则交换
- 删除最后一个节点
代码
https://github.com/Allenxuxu/dsa/blob/master/heap/heap.go
堆排序
堆排序是借助“堆”这种数据结构进行排序的排序算法。
实现
- 将原数组构造成堆
- 将堆顶元素和数组最后一个元素交换,然后执行下沉操作修复堆(此时修复的堆长度-1,最后一个元素用来存放有序数据)
- 重复上述步骤,直至堆为空
代码
https://github.com/Allenxuxu/dsa/blob/master/sort/heapsort.go
type Interface interface {
// Len is the number of elements in the collection.
Len() int
// Less reports whether the element with
// index i should sort before the element with index j.
Less(i, j int) bool
// Swap swaps the elements with indexes i and j.
Swap(i, j int)
}
func down(data Interface, root, n int) {
for {
child := 2*root + 1 // left child
if child >= n {
break
}
if child+1 < n && data.Less(child, child+1) {
// right = child+1
child++
}
if data.Less(child, root) {
return
}
data.Swap(root, child)
root = child
}
}
func HeapSort(data Interface) {
n := data.Len()
// Build heap with greatest element at top.
for i := n/2 - 1; i >= 0; i-- {
down(data, i, n)
}
// Pop elements, largest first, into end of data.
for i := n - 1; i >= 0; i-- {
data.Swap(0, i)
down(data, 0, i)
}
}
应用
堆排序是唯一能够同时最优化的利用空间和时间的方法 – 在最坏的情况下也能保证使用 2NlogN 次比较和恒定额外空间。
但是,现代系统中许多应用很少使用它,因为它无法利用缓存 – 数组元素很少和相邻的元素进行比较。因此缓存命中次数远低于在相邻元素进行比较的算法,如快速排序,归并排序,甚至是希尔排序。